OCAML – TP 3 – les arbres
Exercice 1
Partie 1
Définir un type arbreb pour représenter des arbres binaires dont les éléments peuvent être de n'importe quel type.
Partie 2
Déclarer une variable qui représente l'arbre suivant :

Partie 3
Définir une fonction egalarbre qui teste l'égalité de deux arbres binaires (on suppose que les valeurs présentes dans les arbres peuvent être comparées avec l'opérateur =).
Partie 4
Définir une fonction memestrcuct qui teste si deux arbres binaires ont la même structure (on ne tient pas compte des valeurs).
Partie 5
Définir une fonction hauteur qui calcule la hauteur d'un arbre binaire. La hauteur d'un arbre est la distance maximale entre les feuilles et la racine - 4 dans l'exemple ci dessus.
Partie 6
Définir une fonction mirroir qui construit le mirroir d'un arbre binaire.
Exercice 2
On dit qu'un arbre binaire A est ordonnée quand, pour chacun de ses noeuds N, la valeur de N est supérieure à toutes les valeurs de son sous-arbre gauche et inférieure à toutes les valeurs de son sous-arbre droit. Voici un exemple d'arbre ordonnée :
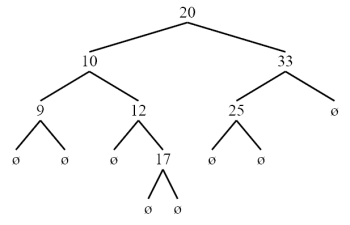
Partie 1
Définir une fonction listevaleurs qui créé une liste des valeurs contenues dans un arbre binaire par un parcours en profondeur.
Partie 2
Définir une fonction estdans de type 'a arbreb -> 'a -> bool, qui teste si une valeur v est présente dans un arbre binaire ordonné.
Partie 3
Définir une fonction insere de type 'a -> 'a arbreb -> 'a arbreb, qui qui insère une valeur dans un arbre binaire ordonné, de telle façon que le résultat soit un arbre binaire ordonné.
Partie 4
Construire un arbre binaire ordonné d'entiers en partant de l'arbre vide et en insérant successivement un certain nombre d'entiers. Puis appliquer la fonction listevaleurs de la partie 1 sur cet arbre. Qu'observe-t'on ?